New blog in 2024 #
After 21 years of blogging here on Blogger.com/Blogspot.com, I decided I should integrate blogging into my main site. I think it will be easier for me to write blog posts that reuse my existing site infrastructure than for me to come here to a separate site to blog.
- New blog is https://www.redblobgames.com/blog/.
- Blog feed is https://www.redblobgames.com/blog/posts.xml.
It's not nearly as featureful as Blogger but it's easy for me to write, and I think I will blog more if there's less friction. My goal is to share more on my blog and less that's limited to Twitter/Discord/Reddit.
I had wanted to do more — migrate my old blog posts to the new site, add categories, add browsing by date — but I decided if I waited until I had everything I wanted, I might never switch to the new blog. So I have launched the new blog with just the minimum (home page and feed), and will consider adding the other things later.
Labels: future
What I did in 2023 #
It's time for my annual self review. In last year's review I said I didn't have clear goals for 2023, and I would probably just do whatever was interesting. I did a bunch of interesting things. Unlike last year, I didn't spend much time on art or science. The first part of the year I was learning about drag & drop on the web. Then I worked on map generation. and the last part of the year were productive, but I felt kind of aimless in the middle.
Labels: annual-review
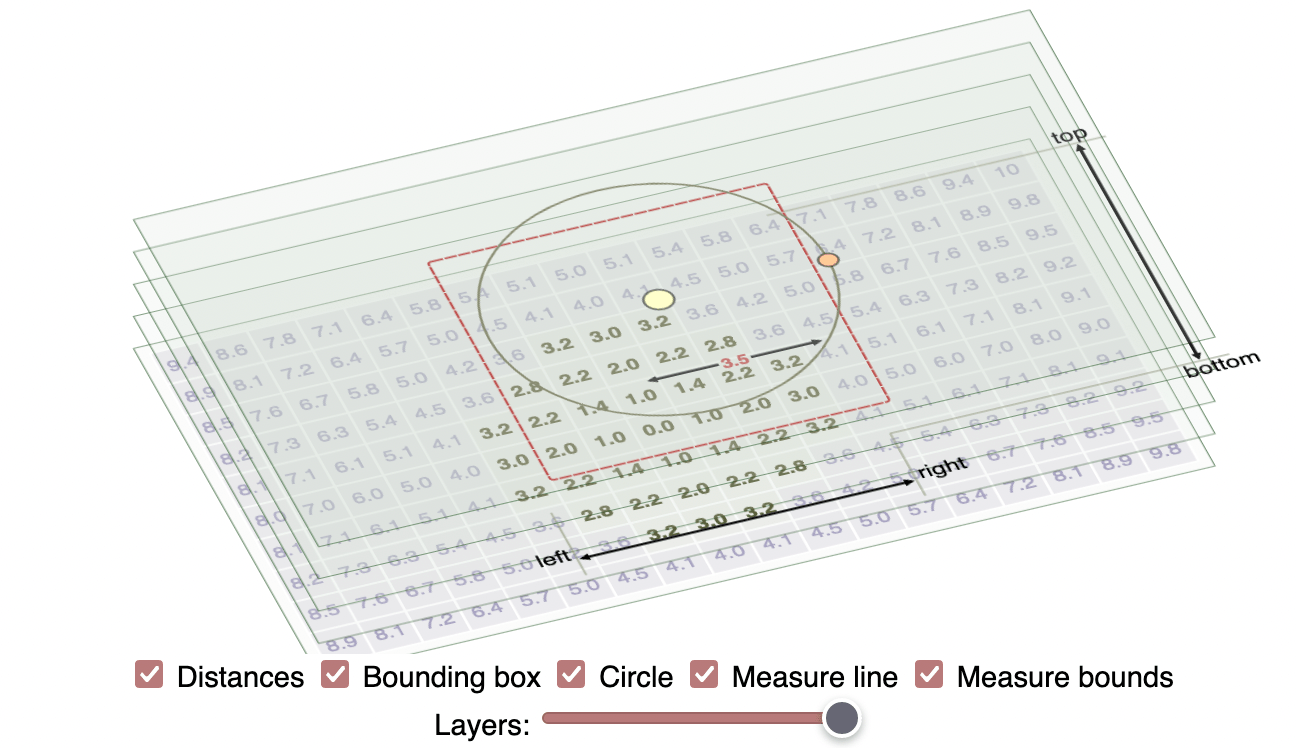
Jobs table implementation for r/roguelikedev project #
In the last post I mentioned that while working on my colony simulator game for the r/roguelikedev summer event, I ran into a situation where my data structures made me unhappy. I was implementing a job system, where a colonist would keep track of what job they're doing, what items they're holding, and where they are standing. It looked like this before I rewrote it:
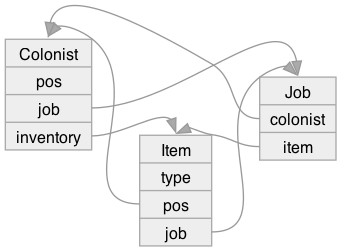
Labels: programming , structure
Summer r/roguelikedev event #
Each summer the r/roguelikedev community has a summer event in which we all make a simple roguelike, roughly following the Python libtcod roguelike tutorial. Last year I tried to clone Dwarf Fortress in 40 hours. That was too ambitious. But I did enjoy working on a "fortress mode" project more than an "adventure mode" project, so I wanted to do something like that this year, but with a smaller scope.
- Event announcement
- Event conclusion from the participants
- Event summary from the organizers
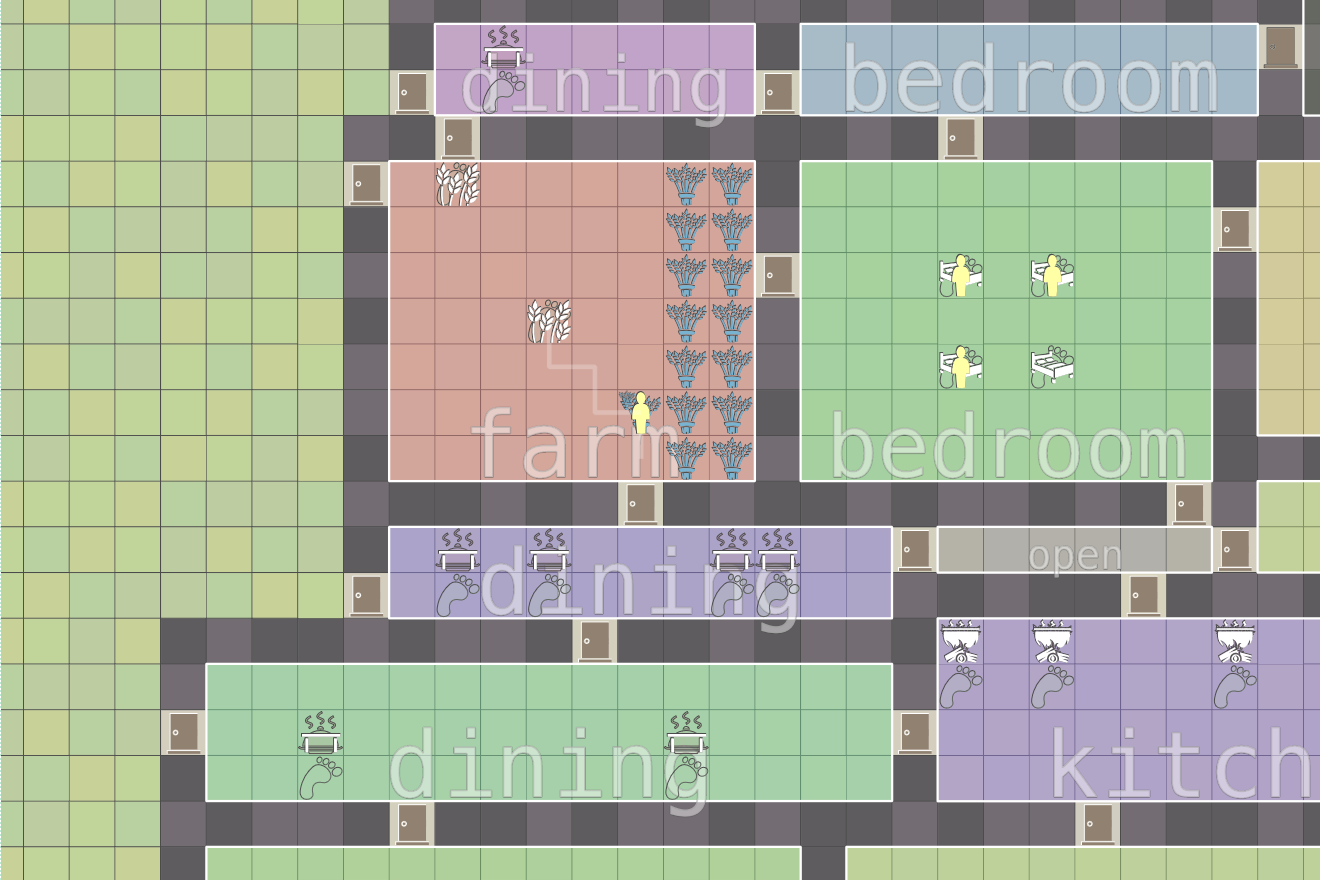
Labels: programming
Writing HTML by hand #
I write some of my pages using a markup language (emacs org-mode) and other pages using xhtml, with a few extra x:* tags that get expanded out into html later. I was curious, when I write html by hand, which tags do I use? I used Python's elementtree to get the answer:
3085 p 2466 a 2303 li 1042 em 1008 code 876 span 719 x:section 517 br 454 div 446 strong 424 h3 410 figure 359 ul 358 script 331 img 323 pre 262 td 249 x:document 228 x:footer 219 g
A lot of what I write is explanations in <p> paragraphs and <ul> <li> lists. And I try to include lots of <a> links to other supporting documents. I do try to use the semantic <em> and <strong> instead of the visual <i> and <b>. These results didn't surprise me much.
Here's the code (roughly):
tag_counts = collections.Counter() for doc in documents: tree = etree.fromstring(doc.contents) for el in tree.iter(): tag_counts[el.tag] += 1 for (tag, count) in tag_counts.most_common(20): print(f"{count:5} {tag}")
Do you write HTML by hand? If so, what tags do you use most?
Update: [2023-09-20] Some people commented on HackerNews about how they write their HTML, including some debate over closing tags, HTML vs XHTML, and markup languages.
Changing a URL #
One of the things I highly value is stable URLs. When you link to my site, I want that URL to work as long as my site is up. I don't want to lose all those links lightly. But for ease of implementation, the URL structure matches the file structure on my site, and I occasionally want to change the file structure. So what should I do?
I make a 301 redirect from the old URL to the new URL.
There are links on forums, discord, stackoverflow, etc. that I can't expect anyone to change. But I can keep those links working on my end by adding a redirect. I have made 28 of these URL changes in 28 years, an average of once year, and each one has a redirect to keep the old URLs working.
Labels: infrastructure
Experiments and motivation #
I was encouraged back in March when I was able to port my tank control experiments from Flash to HTML5. I had previously attempted to port my spaceship control experiments from Flash to HTML5, but failed. Part of the problem was that it wasn't a strict port; I wanted to use a different algorithm. But it didn't work well.
Labels: project
Improving Mapgen4's boundaries, part 3 #
In the last post I described how I investigated and fixed several bugs in mapgen4's boundary points and rendering. I was a bit annoyed at myself because I didn't initially follow great practices while debugging, so it took longer than it should have. But I was also glad I found and fixed the bugs.
One reason I wanted to try a double boundary layer was that I thought it might be neat to "fold" the edges downwards a bit, so that when you look at the map from the side, it'd have some depth. So I tried it, and … it worked! And it was so easy (after I fixed the earlier bugs). I then changed the underground color and added a faint line at the fold:

Improving Mapgen4's boundaries, part 2 #
Last time I mentioned that I made some changes to my dual-mesh helper library. I use it for my Delaunay/Voronoi map and art projects. Part of the motivation was that I want to work on some new map projects, and wanted to fix some of the issues with the library. I then realized I need to test out the changes in mapgen4.
I made a list of mapgen4 bugs I wanted to fix. The main one I'm going to talk about here is that the edges of the map are jagged. Why didn't anyone notice? Because I set the default zoom level to be slightly zoomed in, so that you don't see the edges!

Improving Mapgen4's boundaries, part 1 #
I've been wanting to refamiliarize myself with the mapgen4 code because I'd like to do some new map projects and will want to reuse some of the code from my existing projects.
The first thing I decided to work on was my dual-mesh library. I had originally written it to be a generally useful wrapper around Delaunator. Since then, I wrote the Delaunator Guide, which has all the same functions, but in a way that you can adapt to your own needs. I also realized that by making this library public, I was making it harder for my own needs. So version 3 of this library is going to be primarily for my own needs.
